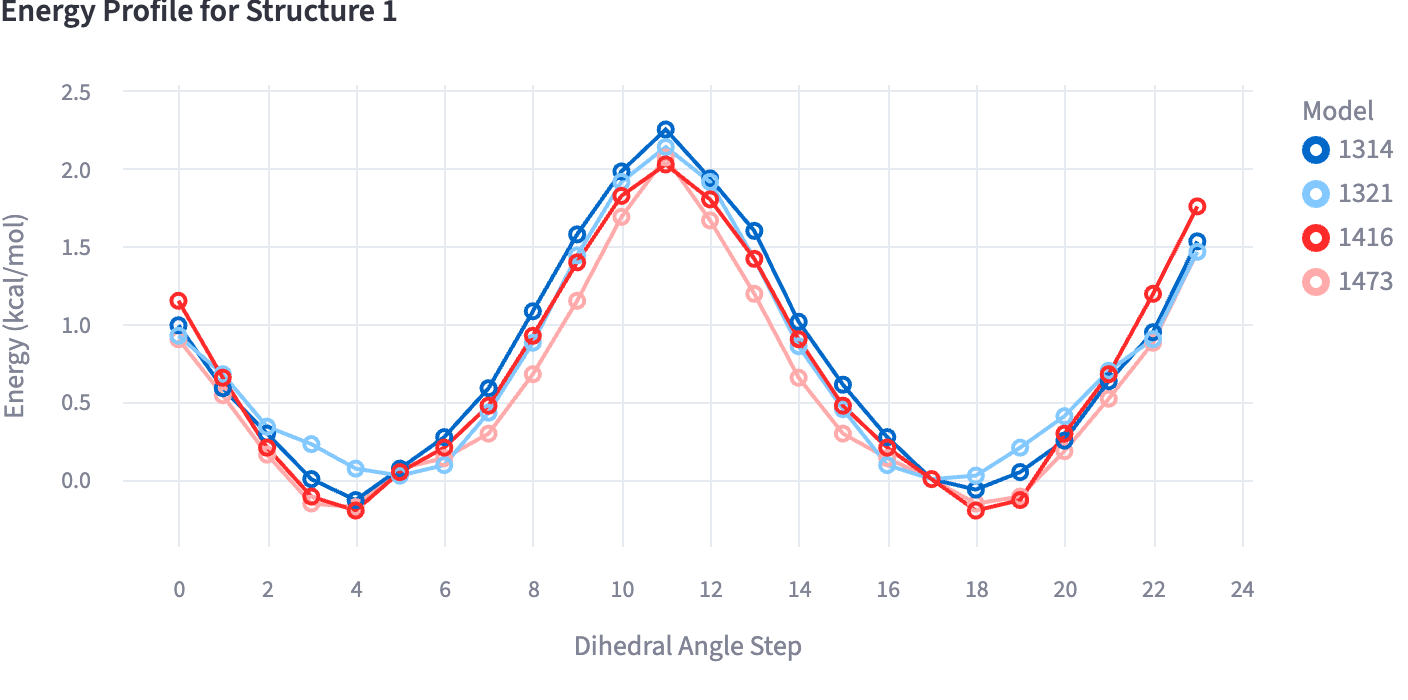
Dihedral scan¶
Purpose¶
This benchmark evaluates the MLIP’s ability to reproduce torsional energy profiles of rotatable bonds in small molecules, aiming to approach the quantum-mechanical QM reference quality.
Description¶
For each molecule, the benchmark leverages the mlip library library for model inference, comparing the predicted energies along a dihedral scan to quantum mechanical QM reference energy profiles. The reference profile is shifted so that its global minimum is zero, and the MLIP profile is aligned to the same conformer. Performance is quantified using the following metrics:
MAE (Mean Absolute Error) and RMSE (Root Mean Square Error) between the MLIP and reference energy profiles.
Pearson correlation coefficient between the MLIP-predicted and reference datapoints.
Mean barrier height error: For each energy profile, the maximum energy relative to the energy minimum is calculated as the barrier height. The absolute error between MLIP and reference barrier heights is computed, and the mean over the full dataset is reported.
These metrics assess the MLIP’s ability to accurately reproduce quantum mechanical torsional energy landscapes, which is critical for modeling conformational energetics and barriers in small molecules.
Dataset¶
The TorsionNet500 [1] dataset consists of 500 drug-like organic molecules with systematically sampled dihedral angles.
Interpretation¶
The correct representation of energetic barriers along conformational changes, like dihedral rotation, is important for simulation-based methods and also to correctly represent transition states of any reaction involving conformational changes. The MAE (Mean Absolute Error) and RMSE (Root Mean Square Error) should be as low as possible and match the expectations from training and testing of the energy inference. The Pearson correlation should be close to 1, but since energy differences between conformers along a dihedral scan may be small, this criterion can be considered a bit less strict than the criterion given for conformational sampling. The mean barrier height error should also be as low as possible and match the expectations about the MLIP’s energy inference.