Radial Distribution Function

Purpose

This benchmark assesses the ability of machine-learned interatomic potentials (MLIP) to accurately reproduce the radial distribution function (RDF) of liquids. The RDF characterizes the local and intermediate-range structure by describing how particle density varies as a function of distance from a reference particle. Accurate modeling of the RDF is essential for capturing both short-range ordering and long-range interactions, which are critical for understanding the microscopic structure and emergent properties of liquid systems.

Description

The benchmark performs an MD simulation using the MLIP model in the NVT ensemble at 300 K for 500,000 steps, leveraging the jax-md engine from the mlip library. The starting configuration is already equilibrated. For every specific atom pair (e.g., oxygen-oxygen in water) the radial distribution function (RDF or g(r)) is calculated from the simulation.

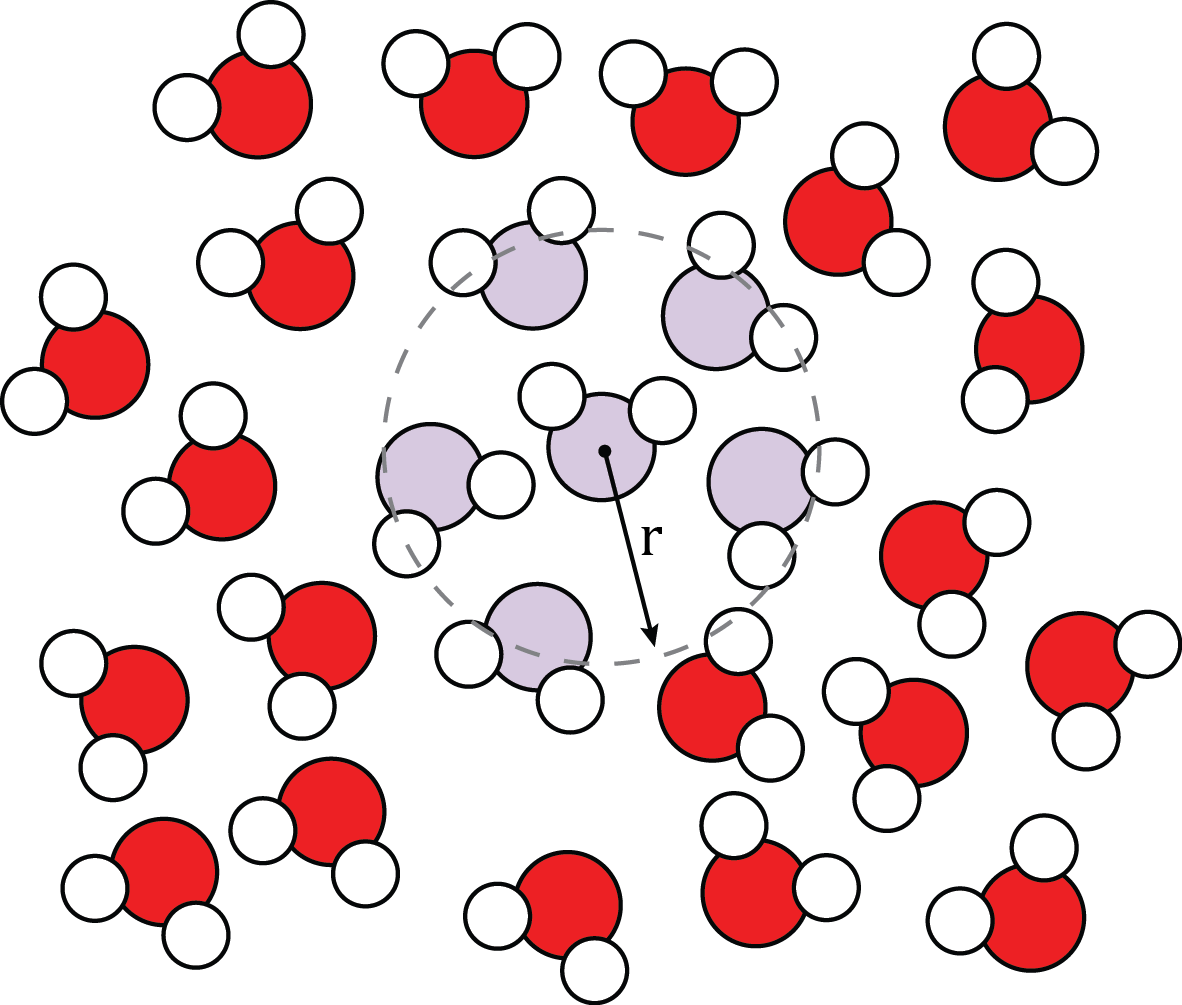
Water Radial Distribution Function Image taken from Wikimedia under a CC BY-SA 4.0 license.

The RDF, \(g(r)\), is defined as:

\[g(r) = \frac{1}{4\pi r^2 \rho N} \left\langle \sum_{i=1}^N \sum_{j \neq i}^N \delta(r - r_{ij}) \right\rangle\]

where:

• \(r\) is the distance from a reference particle,

• \(\rho\) is the average number density,

• \(N\) is the number of particles,

• \(r_{ij}\) is the distance between particles \(i\) and \(j\),

• \(\delta\) is the Dirac delta function,

• and the angle brackets denote an ensemble average.

For each system, the benchmark compares MLIP-predicted RDF against experimental reference data. Performance is quantified using the following metrics:

• Mean Absolute Error (MAE)

• Root Mean Square Error (RMSE)

Dataset

For the water radial distribution benchmark we set up a cubic box of 500 water molecules using OpenMM and the TIP3P water model. We equilibrated the box in the NPT ensemble at standard conditions and extracted the final snapshot as input for the benchmark. For the solvent radial distribution benchmark, we initialized the solvent boxes (methanol, acetonitrile, CCl4) by stacking randomly rotated molecules to yield a cubic box with a target side-length of 28 Å at the experimental density. We equilibrated the box in the NPT ensemble using the GAFF force field and OpenMM.

We use the experimental water RDF profile of Skinner et al.[1] as reference data. For other solvents (methanol[2], acetonitrile[3], CCl4[4]), we use the location of the first solvation shell peaks as reference data.

Interpretation

The MAE and RMSE of the RDF should be as low as possible. These metrics are likely to vary significantly for different molecular liquids and temperature conditions. The error should be compared per liquid type and then examined in more detail for specific molecular interactions to identify areas where the MLIP struggles to reproduce the correct structure. Within these problematic regions, individual RDF profiles can be visually inspected to understand how the MLIP predictions deviate from experimental or reference data.

References

[1]

12. 2. Skinner et al., J. Chem. Phys. 138, (2013). DOI: https://doi.org/10.1063/1.4790861

[2]

10. 23. Handgraaf et al., Chem. Phys. Lett. 367, (2003) DOI: https://doi.org/10.1016/S0009-2614(02)01779-7

[3]

19. Pothoczki et al., J. Mol. Liq. 225, (2017) DOI: https://doi.org/10.1016/j.molliq.2016.11.056

[4]

11. Nishikawa et al., Bull. Chem. Soc. Japan 52, (1979) DOI: https://doi.org/10.1246/bcsj.52.293